Authors:
(1) Antti Autio, Department of Mathematics and Systems Analysis, Aalto University;
(2) Henrik Garde, Department of Mathematics, Aarhus University;
(3) Markus Hirvensalo, Department of Mathematics and Systems Analysis, Aalto University;
(4) Nuutti Hyonen, Department of Mathematics and Systems Analysis, Aalto University.
Table of Links
- Abstract and 1 Introduction
-
- Linearization of the CM of EIT
-
- Explicit representation for F and its inverse
-
- Regularization for truncated systems
-
- Simulating data on piecewise smooth domains and with the CEM
-
- Numerical experiments
-
- Concluding remarks and References
Abstract
This work implements and numerically tests the direct reconstruction algorithm introduced in [Garde & Hyv¨onen, SIAM J. Math. Anal., 2024] for two-dimensional linearized electrical impedance tomography. Although the algorithm was originally designed for a linearized setting, we numerically demonstrate its functionality when the input data is the corresponding change in the current-to-voltage boundary operator. Both idealized continuum model and practical complete electrode model measurements are considered in the numerical studies, with the examined domain being either the unit disk or a convex polygon. Special attention is paid to regularizing the algorithm and its connections to the singular value decomposition of a truncated linearized forward map, as well as to the explicit triangular structures originating from the properties of the employed Zernike polynomial basis for the conductivity.
Keywords: electrical impedance tomography, linearization, direct reconstruction, Zernike polynomials, singular value decomposition
1. Introduction
In electrical impedance tomography (EIT) the aim is to gain information on the conductivity distribution inside a physical body from current and potential measurements on its boundary; see the review articles [2, 4, 22] and the references therein for more information on EIT. The reconstruction problem of EIT can be mathematically formulated as the ill-posed task of inverting the nonlinear operator that maps the internal conductivity of the examined body to the boundary measurements.
The main goal of this paper is to implement and numerically test the direct reconstruction algorithm for two-dimensional EIT introduced in [10, Theorem 1.3], capable of rapidly reconstructing any (even unbounded) L 2 -perturbation to a homogeneous background conductivity. The article [10] only considered the idealized continuum model (CM) of EIT that allows current input and potential measurement everywhere on the object boundary. In this work, we also test the algorithm on data simulated by resorting to the complete electrode model (CEM) [5, 20] as well as on real-world data from a water tank [13]. Moreover, even though the reconstruction algorithm was originally designed for a linearized version of EIT, our numerical studies are exclusively based on difference data corresponding to the nonlinear forward map of either the CM or the CEM. The aim is to demonstrate that an algorithm based on a linearization can systematically produce good quality reconstructions in EIT.
The basic version of the algorithm is formulated assuming the examined object is modeled as the unit disk D, but it can also be applied to any smooth enough simply-connected domain by resorting to the Riemann mapping theorem, as explicitly outlined in the paragraph following [10, Theorem 1.3]. In the framework of the linearized CM, one assumes that the available data is the Fr´echet derivative of the forward map, evaluated at the unit conductivity, in the direction of the to-be-reconstructed conductivity perturbation. This is a linear operator sending input currents to measured boundary potentials. To be more precise, the algorithm takes as its input the elements in the infinite matrix representation of this boundary map with respect to the standard Fourier basis. As hinted above, in our numerical studies these matrix elements are replaced by those corresponding to the actual change in the Neumann-to-Dirichlet (ND) map when the conductivity inside D is perturbed. The reconstruction algorithm itself is comprised of a set of explicit linear formulas that map the aforementioned matrix elements to the coefficients, cj,k, in the expansion of the conductivity perturbation in the Zernike polynomial basis [24]; see also [1] for a similar approach.
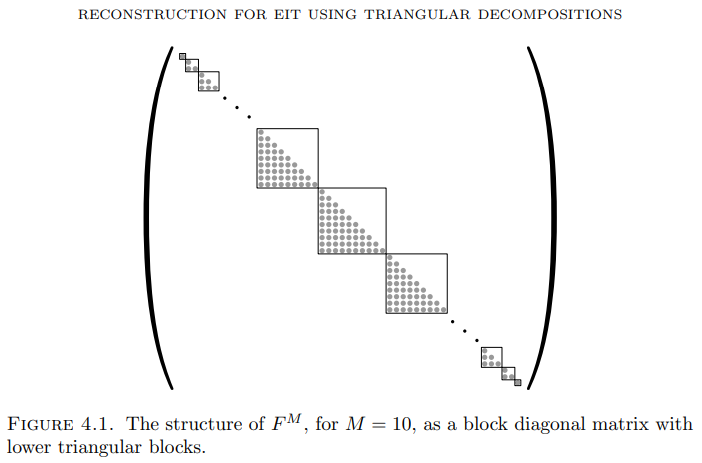
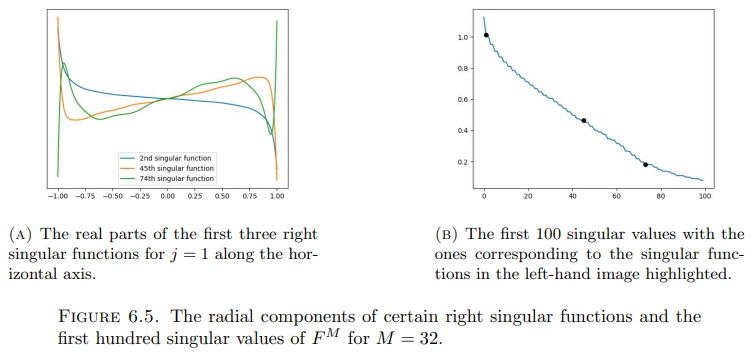
The Zernike polynomials are indexed by two indices: j ∈ Z controlling the Fourier frequency in the polar angle and k ∈ N0 controlling (for a fixed j) the behavior in the radial variable, with increasing k indicating more oscillations closer to the origin. As explicitly proven in [10], reconstructing the coefficients cj,k becomes more unstable as k increases. On the other hand, it turns out that cj,k with a fixed angular index j only affect the jth diagonal in the matrix representation of the associated Frechet derivative. In consequence, a certain angular frequency in the conductivity perturbation can be reconstructed by only considering a single diagonal in the data matrix, and the whole reconstruction algorithm can thus be decoupled into independent smaller tasks indexed by j. What is more, the linear dependence of the jth diagonal in the data matrix on cj,k can be represented by an infinite triangular matrix. The formulas comprising the direct reconstruction algorithm correspond to explicitly inverting these triangular matrices for all j ∈ Z. Note that singular vectors of the linearized forward map must also obey such a decoupling, that is, a right-hand singular vector may only contain a single angular frequency and a left-hand singular vector can only have nonzero elements on a single diagonal of its matrix representation.
The decoupling of the angular frequencies allows, in particular, to separately regularize the subsystems corresponding to different angular indices j. This leads to increasing level of regularization as a function of |j|. Numerically considering radial indices beyond, say, k = 15, is impractical due to the increasing ill-posedness of the subproblems for higher radial indices. Hence, any reasonable regularization method can be used for the decoupled subproblems without loosing the instantaneous nature of the reconstruction algorithm. We consider two simple approaches accompanied by the Morozov discrepancy principle:
(i) truncated singular value decomposition (SVD) and
(ii) choosing the sizes of the decoupled subsystems as a function of |j| by monitoring the absolute values of the elements on their diagonals.
The former has a better theoretical justification, but it cannot fully exploit the triangular structure of the decoupled systems as can the latter.
1.1. Article structure. Section 2 introduces the linearized CM for the unit disk and extends it for square-integrable conductivity perturbations following [10]. In Section 3, the linearized forward map is written out explicitly with respect to the Zernike polynomial basis for the conductivity perturbation and the Fourier basis for the boundary measurements. In addition, the triangular structures of the subsystems corresponding to different angular Zernike indices are studied. The implementation of regularized reconstruction algorithms are considered in Section 4, while Section 5 explains how data for the algorithm can be measured/simulated on polygonal domains or based on the CEM. The numerical experiments are presented in Section 6.
2. Linearization of the CM of EIT

3. Explicit representation for F and its inverse
In this section, we continue to assume that the investigated domain is the unit disk D and give an explicit representation for the bounded linear map

3.2. Matrix representation of the linearized model. Our reconstruction algorithm is based on the fundamental observation that most matrix elements in (3.3) vanish. Indeed, [10, Eq. (4.5)] immediately gives



4. Regularization for truncated systems
This section discusses the implementation of regularized reconstruction algorithms based on truncations of the triangular systems (3.11). To this end, we introduce the notation.




4.2. Truncation of the triangular subsystems. A downside of truncated SVD is that it does not fully exploit the triangular structure of (4.1) and, in particular, the explicit solution formula (3.14). Our second regularization approach aims to address this shortcoming by directly resorting to (3.14), but only up to a |j|-dependent threshold for the radial index k.

5. Simulating data on piecewise smooth domains and with the CEM
In this section, we explain how data measured on more general planar domains or via electrode measurements can be used as input for the regularized algorithms introduced in the preceding section. Although the algorithms have been designed for linearized measurements, all data used as their input in this work are obtained from boundary potential measurements corresponding to nonlinear forward models of EIT.


All employed CM data for the unit disk, i.e., Ω = D, are simulated by choosing Φ = Id in the above scheme. Hence, also with D as the examined domain, the data used as the input for the reconstruction algorithms of Section 4 correspond to a nonlinear forward model in our numerical tests.

Remark 5.1. In our numerical experiments with electrode measurements, the imaged object is the unit disk with equiangular electrodes for simulated data and a water tank with the shape of a right circular cylinder for real-world measurements [13]. The considered conductivity distributions inside the water tank are homogeneous in the vertical direction, as are the rectangular electrodes that are equiangularly attached to lateral surface of the tank and extend from its bottom to the water surface. Due to certain symmetries, such three-dimensional water tank measurements can be modeled with the two-dimensional CEM in the unit disk, cf., e.g., [15].

6. Numerical experiments








First, the truncated SVD algorithm described in Section 4.1 is run on the noiseless data with minimal truncation. According to a subjective visual inspection over many truncation indices, p = 492 gives a close to optimal reconstruction that is shown in Fig. 6.6b and demonstrates that the support of a target inclusion can indeed be faithfully reconstructed despite the employed linearization if the available data is very accurate, cf. [12]. This conclusion remains valid even for inclusions with higher contrasts. Although the reconstruction in Fig. 6.6b also reproduces the conductivity level of the inclusion rather accurately, this would no longer be the case if the conductivity of the inhomogeneity differed considerably more from the background value, due to the linearization error.
Next both the truncated SVD method and the algorithm based on truncation of triangular subsystems from Section 4.2 are applied to data with 1% of additive noise. We set ω = 1 in (4.5) and (4.7), which means that there is no attempt to compensate for the employed linearization or numerical errors via the choice of the fudge factor. The resulting reconstructions are shown in Fig. 6.6c and Fig. 6.6d, and they correspond to the truncation indices p = 174 and p = 154 in the respective algorithms. In particular, far fewer Zernike coefficients are considered in Figs. 6.6c and 6.6d than in Fig. 6.6b. The two regularization methods seem to work about equally well, with the SVD-based approach better recapturing the unperturbed background but being worse at estimating the strength of the conductivity perturbation.
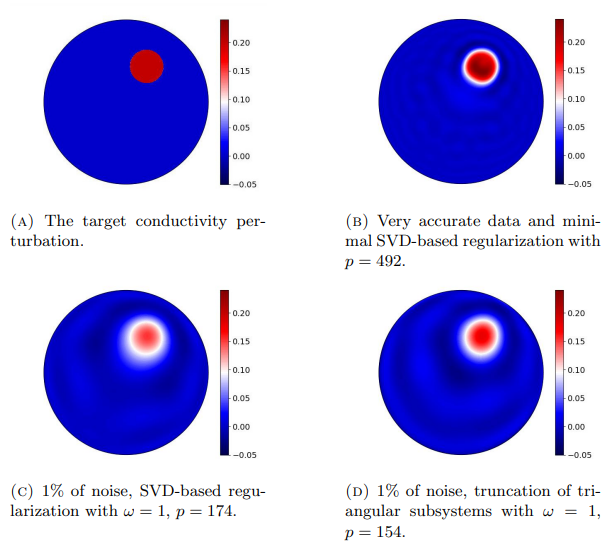

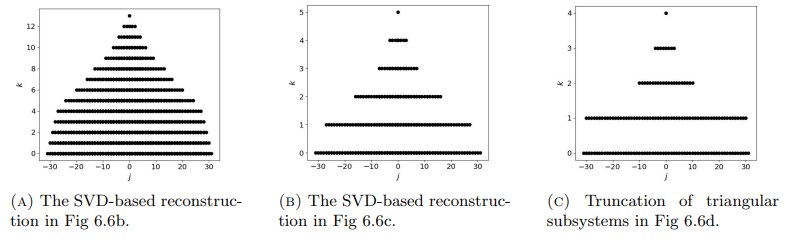

Figure 6.8a illustrates the unit disk with a target conductivity perturbation that behaves as a sine wave with amplitude 0.1 in the vertical direction and is homogeneous in the horizontal direction. The other four images in Fig. 6.8 show reconstructions produced by the truncated SVD method (Section 4.1) and truncation of triangular subsystems (Section 4.2) for the noise levels of 1% and 10%. The SVD-based reconstructions still correspond to the trivial choice ω = 1 in (4.5). However, for the truncation of triangular subsystems, the fudge factor needs to be manually tuned in (4.7) to enable reasonable reconstructions, leading to the heuristic choices ω = 60 and ω = 7, respectively, for the lower and higher noise levels.
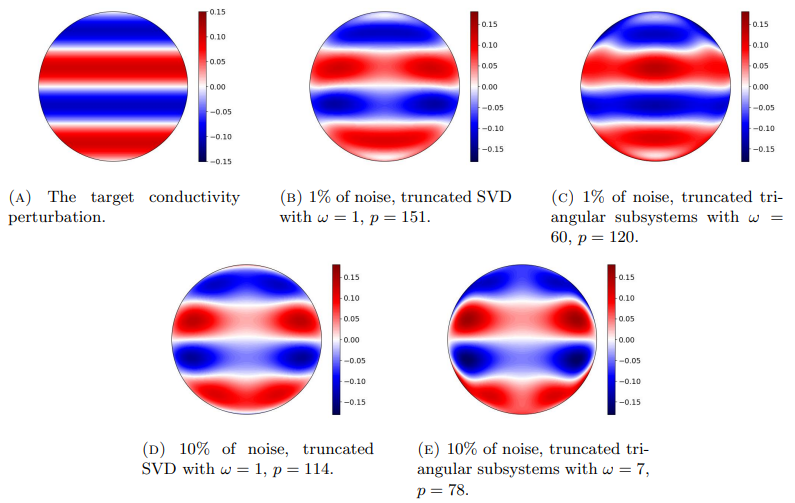
The reconstructions in Fig. 6.8 are able capture the qualitative structure of the target conductivity for both noise levels, although the periodic pattern is somewhat distorted in all reconstructions. This effect is most visible close to the boundary and center of the domain, with reconstructions with the higher noise level suffering from stronger artifacts in this regard. Be that as it may, Fig. 6.8 demonstrates that ignoring the linearization error may still lead to useful reconstructions in EIT even if the supports of the to-be-reconstructed conductivity perturbations are not restricted to the interior of the imaged domain.

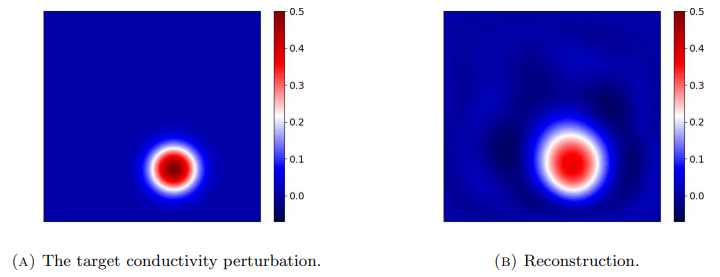
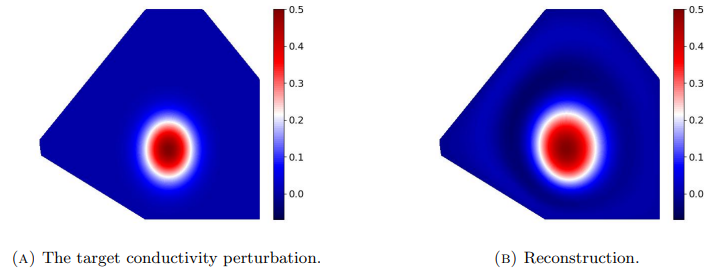
The considered conductivity perturbations are smooth Gaussian humps centered so far from the boundary that their supports are compactly contained in Ω within the numerical precision. The SVD-based algorithm, with ω = 1, is applied to simulated data with 1% of additive noise to produce the reconstructions on the right in Figs. 6.9 and 6.10. Although the algorithm finds the positions of the Gaussian humps, the reconstructions are not as localized as the target perturbations, and they also exhibit wave-like artifacts in the background.

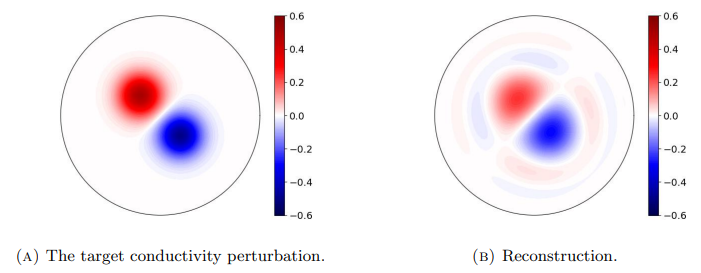
6.5. Water tank measurements. In the final experiment, we consider data from a right cylindrical water tank with 16 electrodes documented in [13]. Note that all measurements in [13] are performed with electrodes that are homogeneous in the vertical direction and extend from the bottom of the tank exactly up to the water surface. The embedded inclusions are also homogeneous in the vertical direction and break the water surface, and they are either perfect insulators (plastic) or can be modeled as ideal conductors (metal). Due to the insulating, i.e., homogeneous Neumann, boundary conditions at the bottom and top of the water layer, the measurements can thus be modeled by the two-dimensional CEM in the unit disk. Moreover, conductivity perturbations reconstructed by resorting to such a model could be presented in the SI units by appropriately scaling with the dimensions of the tank and the conductivity of the saline filling the tank. However, since it is not clear what the precise value for the conductivity of the saline is in [13], the presented reconstructions are to be understood as changes to the unit conductivity inside the unit disk without a proper interpretation in SI units.

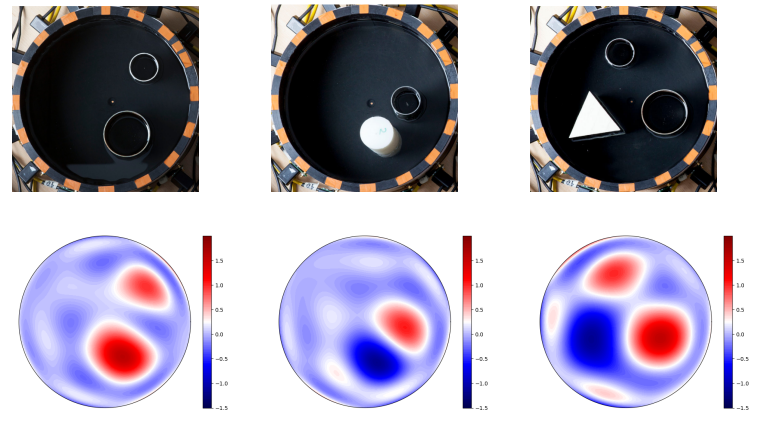
We choose M = 8 and apply the SVD-based reconstruction algorithm to the three sets of data corresponding to the configurations on the top row of Fig. 6.12. Since we do not know the noise level (or the noise model) exactly, we decide to tune the truncation index p via trial and error so that each of the three reconstructions is as good as possible according to a subjective visual inspection. The resulting reconstructions are shown on the bottom row of Fig. 6.12. According to our noise model and the Morozov discrepancy principle, the used regularization parameters correspond to noise levels between 0.1% and 1%. Although the reconstructions in Fig. 6.12 are not based on any systematic way of choosing the level of regularization, they in any case demonstrate that the presented algorithm can under optimal circumstances produce reasonable reconstructions in practical EIT.
7. Concluding remarks
This paper introduced, implemented and numerically tested two regularized variants of the direct reconstruction method for the linearized CM of two-dimensional EIT presented in [10]. Both algorithms exploit the possibility to present the linearized problem in the unit disk with the help of a block diagonal (infinite) matrix with lower triangular blocks, which enables tackling the triangular subsystems separately in the inversion process. More precisely, one of the regularized algorithms is based on a semi-heuristic truncation of the triangular subsystems and the other one on truncating their SVDs. According to our numerical tests, the latter variant is more stable and capable of producing high-quality reconstructions from accurate simulated data, as well as reasonably good reconstructions from noisy measurements on convex polygonal domains and even from real-world water tank data. In particular, ignoring the linearization error does not seem to significantly impede the practical applicability of the introduced reconstruction method.
Acknowledgments. This work is supported by the Academy of Finland (decisions 353080, 353081, 359181) and the Aalto Science Institute (AScI). HG is supported by grant 10.46540/3120- 00003B from Independent Research Fund Denmark | Natural Sciences.
References
[1] A. Allers and F. Santosa. Stability and resolution analysis of a linearized problem in electrical impedance tomography. Inverse Problems, 15:515, 1991.
[2] L. Borcea. Electrical impedance tomography. Inverse problems, 18:R99–R136, 2002.
[3] A. P. Calderon. On an inverse boundary value problem. In Seminar on Numerical Analysis and its Applications to Continuum Physics, pages 65–73. Soc. Brasil. Mat., Rio de Janeiro, 1980.
[4] M. Cheney, D. Isaacson, and J.C. Newell. Electrical impedance tomography. SIAM Rev., 41:85–101, 1999.
[5] K.-S. Cheng, D. Isaacson, J. S. Newell, and D. G. Gisser. Electrode models for electric current computed tomography. IEEE Trans. Biomed. Eng., 36:918–924, 1989.
[6] T. A. Driscoll. Algorithm 756; a MATLAB toolbox for Schwarz–Christoffel mapping. ACM Trans. Math. Soft., 22:168–186, 1996.
[7] H. Garde. Comparison of linear and non-linear monotonicity-based shape reconstruction using exact matrix characterizations. Inverse Probl. Sci. Eng., 26(1):33–50, 2018.
[8] H. Garde and N. Hyvonen. Mimicking relative continuum measurements by electrode data in two-dimensional electrical impedance tomography. Numer. Math., 147(3):579–609, 2021.
[9] H. Garde and N. Hyvonen. Series reversion in Calderon’s problem. Math. Comp., 91:1925–1953, 2022.
[10] H. Garde and N. Hyvonen. Linearised Calderon problem: Reconstruction and Lipschitz stability for infinite dimensional spaces of unbounded perturbations. SIAM J. Math. Anal., 2024. Accepted, arXiv:2204.10164.
[11] T. Gustafsson and G. D. McBain. scikit-fem: A Python package for finite element assembly. Journal of Open Source Software, 5(52):2369, 2020.
[12] B. Harrach and J. K. Seo. Exact shape-reconstruction by one-step linearization in electrical impedance tomography. SIAM J. Math. Anal., 42:1505–1518, 2010.
[13] A. Hauptmann, V. Kolehmainen, N. M. Mach, T. Savolainen, A. Seppanen, and S. Siltanen. Open 2D electrical impedance tomography data archive, 2017. arXiv:1704.01178.
[14] N. J. Higham. Accuracy and stability of numerical algorithms. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, second edition, 2002.
[15] N. Hyv¨onen and L. Mustonen. Smoothened complete electrode model. SIAM J. Appl. Math., 77:2250–2271, 2017.
[16] N. Hyvonen and L. Mustonen. Generalized linearization techniques in electrical impedance tomography. Numer. Math., 140:95–120, 2018.
[17] N. Hyvonen, L. Paivarinta, and J. Tamminen. Enhancing D-bar reconstructions for electrical impedance tomography with conformal maps. Inverse Probl. Imaging, 12:373–400, 2017.
[18] Ch. Pommerenke. Boundary behaviour of conformal maps. Springer-Verlag, 1992.
[19] J. Saranen and G. Vainikko. Periodic integral and pseudodifferential equations with numerical approximation. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2002.
[20] E. Somersalo, M. Cheney, and D. Isaacson. Existence and uniqueness for electrode models for electric current computed tomography. SIAM J. Appl. Math., 52:1023–1040, 1992.
[21] L. N. Trefethen. Numerical computation of the Schwarz–Christoffel transformation. SIAM J. Sci. Stat. Comput., 1:82–102, 1980.
[22] G. Uhlmann. Electrical impedance tomography and Calderon’s problem. Inverse Problems, 25:123011, 2009.
[23] M. Vauhkonen. Electrical impedance tomography with prior information, volume 62. Kuopio University Publications C (Dissertation), 1997.
[24] F. Zernike. Beugungstheorie des schneidenverfahrens und seiner verbesserten form, der phasenkontrastmethode. Physica, 1:689–704, 1934.
This paper is available on arxiv under CC BY 4.0 DEED license.

